conceptos de circulo y circunferencia
Si me pides una definición más técnica o formal, ésta iría por el lado de definirla como un lugar geométrico, vale decir: una circunferencia es el lugar geométrico de los puntos de un plano, que equidistan de otro punto del mismo plano definido como centro.
En otra palabras: señalo un punto del plano al que determino como centro y todos aquellos puntos del mismo plano que estén a la misma distancia de ese centro, pertenecen (y a la vez conforman) a la circunferencia en cuestión.
Pero lo cierto es que en los primeros años escolares, los docentes tratamos de aportar definiciones más sencillas e intuitivas, que no se aparten del concepto correcto. De este modo, es frecuente que definamos a una circunferencia de un modo más simple, como podría ser: “Una circunferencia es una línea curva cerrada y plana, cuyos puntos están situados a la misma distancia de otro punto del mismo plano, llamado centro.”
Los elementos más importantes en una circunferencia, y sus respectivas definiciones, son los siguientes:
Centro: es el punto medio de una circunferencia, al cual todos sus puntos equidistan
Radio: es un segmento de recta que une al centro con cualquiera de los puntos de la circunferencia
Diámetro: es un segmento de recta que une dos puntos de una circunferencia, pasando por el centro
Semicircunferencia: es cada una de las dos mitades en que queda dividida una circunferencia, cuando ésta es dividida por un diámetro.
Arco: es una porción de circunferencia, comprendida entre dos de sus puntos (que no sean el centro)
Arco: es una porción de circunferencia, comprendida entre dos de sus puntos (que no sean el centro)
Cuerda: es un segmento de recta que une dos puntos de una circunferencia SIN pasar por el centro de la misma.
Llamamos círculo a la superficie del plano que se encuentra contenida dentro de una circunferencia. Comparte -por cierto- algunos de los elementos básicos antes nombrados con la circunferencia, tal es el caso del centro, el diámetro y el radio. Las tres cosas se definen de la misma manera para un círculo y en la imagen de portada podemos visualizar mejor cada concepto.
No podemos decir lo mismo de la semicircunferencia (que hemos definido antes),no obstante lo cual, existe un concepto análogo en el círculo, que es el semicírculo.
Semicírculo: se llama semicírculo a cada una de las dos mitades en que queda dividido un círculo, al trazar un diámetro.
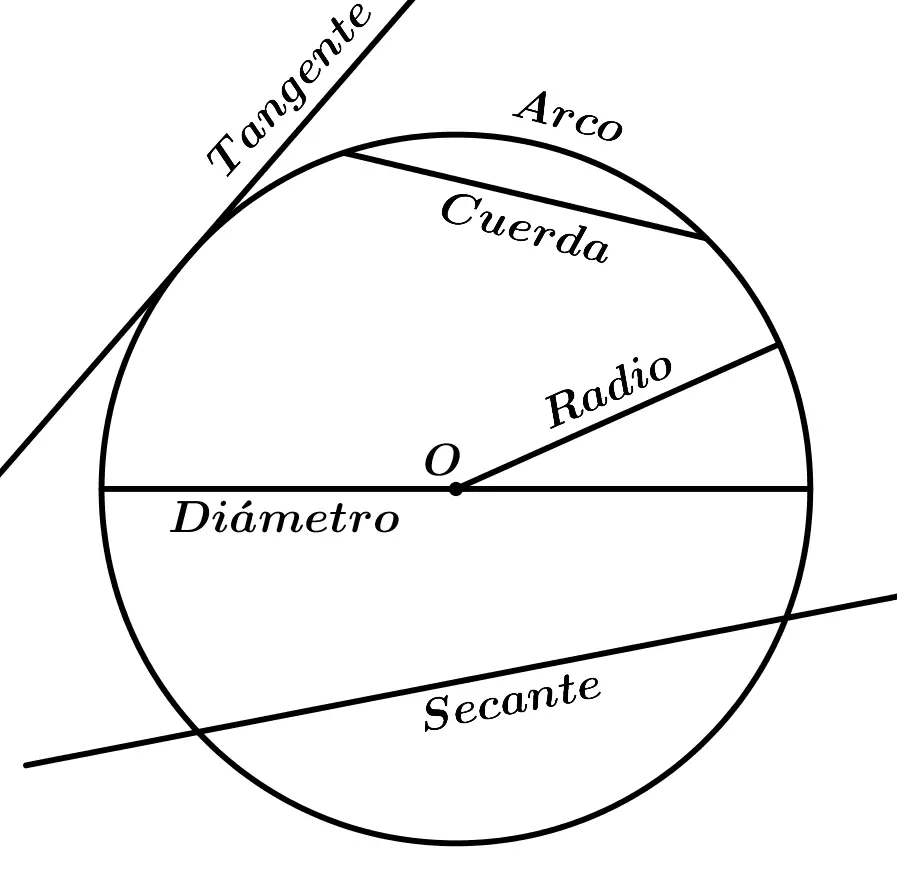
segmentos y rectas de la circunferencia
· Centro, el punto interior equidistante de todos los puntos de la circunferencia.
· Diámetro, el mayor segmento que une dos puntos de la circunferencia y que necesariamente pasa por el centro.
· Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros).
· Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.
En el plano, una recta puede intersecar a una circunferencia en un punto, intersecarse en dos puntos o no intersecarse.
· Las rectas que intersecan a la circunferencia en un solo punto se llaman rectas tangentes a la circunferencia. Al punto en el que la tangente interseca a la circunferencia se llama punto de tangencia; una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro, por lo cual, la distancia que hay del centro a la recta tangente es igual al radio.
· Las rectas que intersecan en dos puntos a la circunferencia se llaman rectas secantes. La distancia del centro de la circunferencia a la recta secante es menor que el radio.
· Las rectas que no intersecan a la circunferencia se llaman rectas exteriores. La distancia del centro de la circunferencia a la recta exterior es mayor que el radio.
El perímetro de un circulo es la circunferencia y su valor es igual diámetro multiplicado por pi. Como el diámetro es igual a dos radios también se puede decir que la longitud de la circunferencia = p x 2r


secciones de un circulo
· Ángulo central tiene su vértice en el centro por lo que sus lados contienen a dos radios. La amplitud de un ángulo central es igual a la del arco que abarca.
· Ángulo inscrito su vértice es un punto de la circunferencia y sus lados son dos cuerdas.
· Ángulo semi-inscrito su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia. La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
· Ángulo interior su vértice está en el interior de la circunferencia. La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.
· Ángulo exterior tiene su vértice en el exterior de la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella.
perímetro de una circunferencia
El perímetro de un circulo es la circunferencia y su valor es igual diámetro multiplicado por pi. Como el diámetro es igual a dos radios también se puede decir que la longitud de la circunferencia = p x 2r

Área de un círculo
Un círculo es el conjunto de todos los puntos en un plano a una distancia dada (llamado el radio ) desde un punto dado (llamado el centro.)
Un segmento de la recta que conecta dos puntos en el círculo y pasa a través del centro es llamado un diámetro del círculo.

Claramente, si d Representa la Longitud de la ONU Diámetro y r Representa la Longitud de Radio de la ONU, ENTONCES d = 2 r .
La circunferencia C de un círculo es la distancia alrededor del exterior. PARA CUALQUIER círculo, this Longitud this Relacionada con el de radio r por la Ecuación
C = 2π r
donde π (pronunciada como " pi ") es una constante irracional aproximadamente igual a 3.14.
El área de un círculo esta dada por la fórmula
A = π r 2 .
secciones de un circulo
El cuadrante y el semicírculo son dos tipos especiales de sectores:
 | Un cuarto de círculo se llama cuadrante. Medio círculo se llama semicírculo. |
 |
El área de un sector
Puedes calcular el área de un sector comparando su ángulo con el ángulo de un círculo completo.
Nota: aquí estoy escribiendo los ángulos en radianes.
|
|
El cálculo de áreas de figuras geométricas se hace útil cuando debemos determinar el área de una región no convencional; es decir, regiones cuya forma no es geométricamente tradicional como los cuadrilateros, triángulos, círculos y polígonos en general.
A veces debemos determinar el área para calcular otras variables como la cantidad y el costo de los materiales con los cuales se construye algo como un edificio (pisos, paredes, ventanas, etc.), o contenedores (cartón , acrílico, madera, entre otros).
En esta unidad se presentan algunas regiones no convencionales para el cálculo de su área. Igualmente se suministran las ayudas necesarias en caso de no conocerse el procedimiento adecuado para dicho cálculo.
Algunas áreas a calcular se muestran a continuación:



No hay comentarios.:
Publicar un comentario